PHY.K03 Solid State Physics Exercise Exam
30.04.2024

(a) Write down the many-electron Hamiltonian (the total Hamiltonian) for carbon ($Z=6$) neglecting Slater's rules.

(b) The many electron Hamiltonian is difficult to solve. Write down an approximate many electron wavefunction for the ground state of carbon. This wavefunction should be properly antisymmetrized.

(d) How could you determine the effective spring constant of an O₂ from the vibrational spectrum?

(e) How many molecular orbitals are filled in the ground state of O₂? (Oxygen has 8 protons and 8 neutrons).

Solution

(a)

$$H_{\text{total}}= - \sum \limits_i^6 \frac{\hbar^2}{2m}\nabla_i^2  - \sum \limits_i^6 \frac{6e^2}{4\pi\epsilon_0 |\vec{r}_i|} + \sum \limits_{i\lt j}\frac{e^2}{4\pi\epsilon_0 |\vec{r}_i-\vec{r}_j| }.$$

(b) A many-electron wavefunction can be written as a Slater determinant.

\begin{equation}
 \Psi(\vec{r}_1,\vec{r}_2,\cdots,\vec{r}_6)= \frac{1}{\sqrt{6!}}\left|\begin{array}{slate} \phi_{1s}\uparrow (\vec{r}_1) & \phi_{1s}\downarrow (\vec{r}_1) & \phi_{2s}\uparrow (\vec{r}_1) & \phi_{2s}\downarrow (\vec{r}_1) &  \phi_{2p_x}\uparrow (\vec{r}_1) & \phi_{2p_y}\uparrow (\vec{r}_1)   \\ 
\phi_{1s}\uparrow (\vec{r}_2) & \phi_{1s}\downarrow (\vec{r}_2) & \phi_{2s}\uparrow (\vec{r}_2) & \phi_{2s}\downarrow (\vec{r}_2) &  \phi_{2p_x}\uparrow (\vec{r}_2) &  \phi_{2p_y}\uparrow (\vec{r}_2)   \\ 
\vdots & \vdots &  & \vdots \\ 
\phi_{1s}\uparrow (\vec{r}_6) & \phi_{1s}\downarrow (\vec{r}_6) & \phi_{2s}\uparrow (\vec{r}_6) & \phi_{2s}\downarrow (\vec{r}_6) &  \phi_{2p_x}\uparrow (\vec{r}_6) &  \phi_{2p_y}\uparrow (\vec{r}_6)   \\  \end{array}\right|. 
\end{equation}

Hund's rules tell us to fill two different $2p$ orbitals before filling the same one with spin $\uparrow$ and $\downarrow$. This is because of electron-electron interactions.

(c) The rotational energy levels are,

$E_J= \frac{\hbar^2}{2I}J(J+1)= BJ(J+1)$ .

The lines in the rotational spectrum have a spacing of $2B$. From $B$ we could calculate the moment of inertia $I=\frac{m_am_b}{m_a+m_b}r_0^2$. Since the mass of the oxygen atom is known, $m_a = m_b = m_O$, we can calculate the distance from the center of mass to the atoms, $r_0$, and this is half the bond length.

(d) Photons emitted due to a transition between vibrational levels have an energy $\hbar\omega = \hbar\sqrt{\frac{k}{m_r}}$ where $k$ is the effective spring constant and $m_r = \frac{m_O}{2}$ is the reduced mass of the molecule. Since the mass of the oxygen atom is known, the effective spring constant can be calculated.

(e) There are 16 electrons in the molecule so 8 molecular orbitals will be occupied.

Problem 2

(a) Which directions are equivalent to [100] in a tetragonal system?

<100> =

(b) Which planes are equivalent to (110) in an orthorhombic system?

{110} =

(c) A plane cuts the crystalographic axes of a crystal at $3\vec{a}$, $4\vec{b}$, and $6\vec{c}$ where $\vec{a}$, $\vec{b}$, and $\vec{c}$ are the primitive lattice vectors. What are the Miller indices of this plane?

(d) Draw the primitive lattice vectors in this periodic pattern.

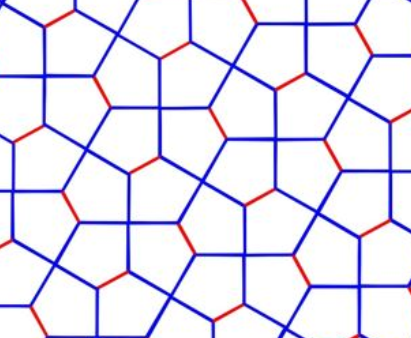
Solution

Problem 3

Two views of the conventional unit cell of hexagonal boron nitride are shown below.

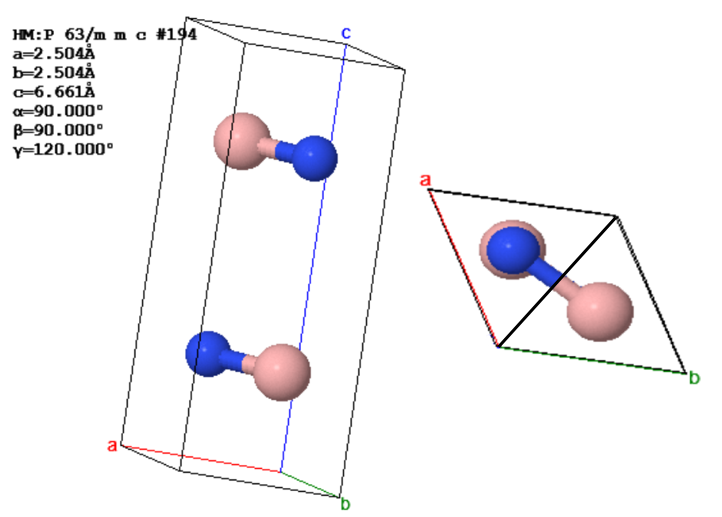
(a) Draw the atoms in the (001) plane.

(b) What is the volume of the conventional unit cell? (Don't forget the units.)

(d) What is the space group of this crystal?

(e) The reciprocal lattice vector $\vec{b}_3$ must be perpendicular to $\vec{a}_1$ (= a in the drawing) and perpendicular to $\vec{a}_2$ (= b in the drawing). What is $\vec{b}_3$? (Don't forget the units.)

Solution

PHY.K03 Solid State Physics Exercise Exam30.04.2024

PHY.K03 Solid State Physics Exercise Exam
30.04.2024