PHY.K03 Solid State Physics Exercise Exam
25.06.2024

Name Matrikelnr.

Each subsections (a), (b), (c), $\cdots$ can be awarded a maximum of 4 points.

Problem 1
You need to design a Bragg mirror that consists of many alternating layers of two transparent materials but should reflect light with an angular frequency of $\omega = 10^{15}$ rad/s. The layers all have a thickness $L$. Light propagates at 2.9 × 10⁸ m/s in one of the materials and 2.0 × 10⁸ m/s in the other material. For long wavelengths $\lambda \gg L,$ light propagates at the average speed of 2.45 × 10⁸ m/s.

(a) What is $k$ at the first Brillouin zone boundary in terms of $L$?

(b) Sketch the dispersion relation $(\omega\text{ vs. }k)$ for this layered material.

(d) How large should $L$ be so that the Bragg mirror reflects light with an angular frequency of $\omega = 10^{15}$ rad/s?

(e) Sketch the solution of the wave equation for $\omega = 10^{15}$ rad/s.

Solution

Problem 2

Polonium is the only element that forms a simple cubic crystal structure. The lattice constant is
$a = 3.359$ Å.

(a) Calculate the primitive reciprocal space lattice vectors.

(b) At which scattering angle 2θ is the diffraction of the 322 reflection observed, if the wavelength of the X-rays is 1.0 Å?

(c) A band structure calculation for polonium is shown below. This calculation was made assuming that the relevant orbits were the 6s and 6p atomic orbitals. Polonium has one atom in the basis and 6 valence electrons. Draw the Fermi energy into the band structure. Explain why you have drawn the Fermi energy where you have.

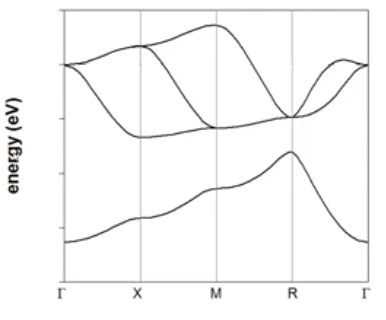
(d) Sketch the phonon band structure ($\omega$ vs. $k$) of polonium. Use the same symmetry points as in the electronic band structure above.

(e) You measure the specific heat $c_v$ of Po experimentally. How can you determine the electron contribution to the specific heat and the phonon contribution to the specific heat separately?

Solution

(a)
 $\vec{b}_1 = \frac{2\pi}{a} \hat{k}_x = 1.87\,\hat{k}_x$ Å-1,

$\vec{b}_2 = \frac{2\pi}{a} \hat{k}_y = 1.87\,\hat{k}_y$ Å-1, 
 $\vec{b}_3 = \frac{2\pi}{a} \hat{k}_z = 1.87\,\hat{k}_z$ Å-1.

(b)
 $|\vec{k}| = \frac{2\pi}{\lambda} = 6.283$ Å-1, $|\vec{G}_{322} |=\sqrt{(3b_1)^2+(2b_2)^2+(2b_3)^2} = 7.71$ Å-1. 
$$\Delta \vec{k} = \vec{G}$$
$$ \frac{G}{2} = k \sin\theta$$

$$ \theta = 0.66\,\text{rad}$$
$$ 2\theta = 1.32\,\text{rad}$$

(c)
<table><tr><td><img src="po3.png" width="300" /></td><td>
There are four bands that can each hold two electrons. The bands will be 3/4 full.
</td></tr></table>

(d) There is one atom in the basis so there will only be 3 acoustic branches to the phonon dispersion. There will be one longitudnal mode and two transverse modes.

(e) At low temperatures the electron contribution to the specific heat is linear in the temperature $c_{v,el} = \gamma T$ and the phonon contribution is cubic in the temperature $c_{v,ph} = A T^3$. The measured specific heat is $c_{v} = \gamma T+A T^3$ If you divide by $T$ and plot $\frac{c_v}{T}$ vs. $T^2$ the result will be a straight line. You can fit this line to determine the parameters $\gamma$ and $A$.

Problem 3

(a) A crystal has 5 atoms in the basis. How many $\vec{k}$ states does this crystal have per primitive unit cell?

(b) ZnO undergoes a structural phase transition from wurzite to zincblende. How could you determine the temperature at which this phase transition occurs?

(c) An electron scatters from state $\vec{k}$ to state $\vec{k}'$ and generates a phonon with wave vector $\vec{k}_{\text{ph}}$. The conservation of momentum for this case is $$\hbar \vec{k}' + \hbar \vec{k}_{\text{ph}}= \hbar \vec{k} + \cdots.$$

What does $\cdots$ represent in this equation?

(d) There is a contribution to the thermal conductivity from the electrons and from the phonons. Why is the thermal conductivity of a metal related to its electrical conductivity?

(e) Use the free electron model to explain how the specific heat depends on the electron density.

Solution

(a) There are two $\vec{k}$ states per primitive unit cell. The 2 is for spin.

(b) Calculate the electron dispersion and phonon dispersion of both phases. From these calculate the electron density of states and the phonon density of states. From the densities of states you can calculate the electron contribution to the Helmholtz free energy and the phonon contribution to the Helmholtz free energy. The temperature where the two free energies are equal is the temperature of the phase transition.

(c) $\hbar\vec{G}$, an electron can change its momentum by a reciprocal lattice vector, $\Delta \vec{k} = \vec{G}$.

(d) While both the electrons and phonons contribute to the thermal conductivity, the electron contribution dominates in metals. The electrons carry the heat current and the electrical current. The diffusion current is coupled to the electrical current through the Einstein relation,

$$ D = \frac{\mu k_BT}{e},$$

where $D$ is the diffusion constant and $\mu$ is the electron mobility. The ratio of the thermal conductivity to the electrical conductivity is the Wiedemann-Franz law,

$$\frac{\kappa}{\sigma T} = L.$$

The Wiedemann-Franz law can be used to estimate the thermal conductivity by measuring the electrical conductivity.

(e) The specific heat depends on the number of states near the Fermi surface. As $n$ increases, the radius of the Fermi sphere increases and therefore the specific heat increases.

PHY.K03 Solid State Physics Exercise Exam25.06.2024

PHY.K03 Solid State Physics Exercise Exam
25.06.2024