Problem 1

(a) Write down a trial wavefunction for a Li₂ molecule using the Linear Combination of Atomic Orbitals.

(b) How many molecular orbitals would be calculated using your trial wave function?

(c) Let's call the molecular orbitals that were calculated for Li₂ $\psi_{\text{mo1}}\cdots\psi_{\text{mo}N}$ with $\psi_{\text{mo1}}$ having the lowest energy and $\psi_{\text{mo}N}$ the highest energy. Write down the ground state as a many electron wavefunction.

(d) Write down the first excited state as a many electron wavefunction. Why is exchange relevant for the excited state?

Problem 2

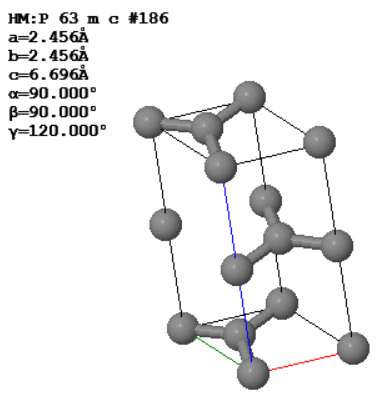
The conventional unit cell of graphite is shown below.

(a) What is the smallest primitive reciprocal lattice vector of graphite?

(b) Use your answer to (a) to calculate the longest wavelength x-rays that could be used to observe a diffraction peak of graphite.

(c) Write down a 3 × 3 matrix that describes a symmetry element of graphite (other than the identity element).

(d) The electrical conductivity of graphite is much higher parallel to the hexagonal planes than perpendicular to them. Use this fact and the Wiedermann-Franz law to discuss the thermal conductivity in graphite. What contributes to the thermal conductivity in this material?

Problem 3

(a) The reciprocal lattice vectors for a crystal are determined in an x-ray diffraction experiment. Then a neutron diffraction experiment is performed. How could you calculate where the neutron diffraction peaks are expected?

(b) In addition to the elastic scattering peaks, there are inelastic neutron diffraction peaks. What information can be determined from inelastic neutron scattering?

(c) What do you measure in a ultraviolet photoemission experiment? Can you tell if a material is metallic or insulating with photoemission? Explain your reasoning.

(d) The electrical conductivity of intrinsic germanium is 2.17 at 20°C. The band gap of germanium is 0.67 eV. What is the conductivity of intrinsic germanium at 30°C?

Problem 4

(a) A metal is simple cubic with a lattice constant $a$ and has one valence electron per unit cell. What is the ratio of the Fermi wavevector to the length of the $\vec{k}$-vector at symmetry point $R$ at the corner of the Brillouin zone?

(b) Write down the general form for an electron wavefunction in the plane wave method.

(c) Near the top of the valence band of an intrinsic semiconductor, the electron dispersion relation is,

$E = $ -$k^2$ [J].

Near the bottom of the conduction the electron dispersion relation is,

$E = $ + $k^2$ [J].

What is the chemical potential at $T=0$ K?

(d) For the semiconductor described in (c), what is the effective mass of the holes in terms of the free electron mass $m_e$? ($e=1.60217733 \times 10^{-19}$ C, $\hbar = 1.05457266 \times 10^{-34}$ Js, $m_e = 9.1093897 \times 10^{-31}$ kg)