Problem 1

The energies of the molecular orbitals for a conjugated ring of $N$ atoms are,

For Benzene, $N=6$ and there are $6$ electrons that occupy these molecular orbitals. Consider what would happen as $N\rightarrow\infty$ and the number of electrons is also $N$. The distance between the atoms is $a$.

(a) Assumming that $H_{11} = -12$ eV, $H_{12} = -4$ eV, and $S_{12} = 0$, for what value of $N$ would the maximum energy level spacing be smaller than $k_BT$ at 300 K?

(b) In the limit of large $N$ would this material be a metal, a semiconductor, or an insulator? Explain your reasoning.

(c) Sketch the electron dispersion relation. Use units of electronvolts on the energy axis and label the wave number axis in terms of $a$.

Problem 2

(a) A bond potential is calculated by evaluating the energy of the ground state wave function as a function of the interatomic distance. How could you tell from the bond potential if the bond is a covalent bond, an ionic bond, or a van der Waals bond?

(b) For a given bond potential, how would you calculate the force between the atoms as a function of distance?

(c) Acetylene contains two carbon atoms and two hydrogen atoms.

acetylene

What kind of bonds are present in acetylene?

(d) How many vibrational modes does acetylene have?

Problem 3

A conventional (cubic) unit cell of zincblende, ZnS, is shown below. Note the similarity to the diamond structure.

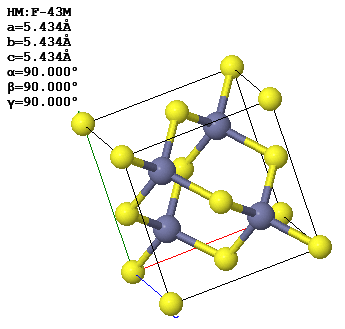
(a) How many atoms of each type are contained in a conventional unit cell?

(b) Give a set of fundamental translation vectors $(\vec{a}_1,\,\vec{a}_2,\,\vec{a}_3)$ which can be used to define the primitive unit cell. How many atoms are there in the primitive cell?

(c) What is the length of the $\vec{G}_{210}$ reciprocal lattice vector? The reciprocal lattice vectors are indexed using the conventional unit cell.

(d) Why does the phonon dispersion relation for silver look like the phonon dispersion relation for copper? Name another material with a similar phonon disperion as copper.

Problem 4

(a) Draw the electron dispersion relation along $L-\Gamma-X$ for aluminum (an fcc metal). Start with the empty lattice approximation and explain how this should be modified to include periodic potential that the electron experiences. For fcc, $\overline{\Gamma L}=\frac{\sqrt{3}\pi}{a}$ and $\overline{\Gamma X}=\frac{2\pi}{a}$.

(b) Aluminum has three valence electrons. Use this information to draw the chemical potential into the dispersion relation you drew.

(c) Sketch the electron density of states based on the dispersion relation you have drawn. Explain why your sketch has this form.

(d) Give an expression for the internal energy density in terms of the density of states.