Problem 1
(a) The molecular orbitals are found by solving the molecular orbital Hamiltonian. What is the molecular orbital Hamiltonian for H2O?
(b) The molecular orbital Hamiltonian can be solved using the method of Linear Combination of Atomic Orbitals. Suppose we assume that we assume that the molecular orbitals for water can be written as a linear combination of the hydrogen 1s orbitals and the oxygen 1s, 2s, and 2p orbitals. How many molecular orbitals would be calculated?
(c) Which of the molecular orbitals of water would be occupied in the ground state many-electron wavefunction?
(d) How would the O-H bond angle be calculated for water?
Problem 2
Derive Bragg's law $2d\sin\theta = n\lambda$ from the Laue condition $\Delta \vec{k} = \vec{G}$.
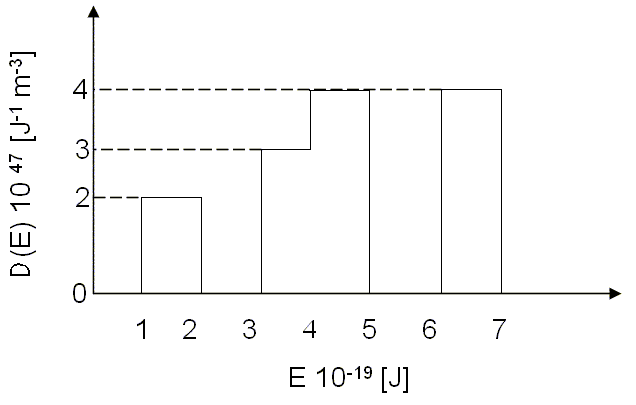
Problem 3
The density of states for a particular material is given in the following figure. The total electron density is 9 × 1028 electrons/m³.

(a) Is this material a metal, an insulator, or a semiconductor? Why?
(b) What is the limiting value of the Fermi energy as the temperature approaches zero?
Problem 4
An intrinsic semiconductor shows the following values for the specific resistivity:
at 145°C ρ = 2 Ω cm,
at 710°C ρ = 3×10-3 Ω cm.
The temperature dependence of the resistivity is mostly determined by the temperature dependence of the carrier density,
$n_i=\sqrt{N_cN_v}\exp \left(\frac{-E_g}{k_BT}\right)$.
If you neglect this temperature dependence of $N_c$ and $N_v$ and assume that the mobilities of the electrons and holes are temperature independent, then you can estimate the band gap of the semiconductor. What is the band gap in this case?