First name
Last name
Matrikelnr.
Problem 1
The molecular orbitals of a water molecule H2O can be calculated using the Linear Combination of Atomic Orbitals method (LCAO). In the trial wave function, the 1s and 2s orbitals of hydrogen are included as well as the 1s, 2s, 2p, 3s, 3p, and 3d orbitals of oxygen. It is necessary to include orbitals up to 3d to get the shape of the molecule correct.
(a) How many molecular orbitals would be calculated using this trial wavefunction?
(b) How many molecular orbitals would be occupied when the molecule is in its ground state? Hydrogen has one electron and oxygen has eight electrons.
(c) How many rotational modes and how many vibrational modes does a water molecule have?
(d) What kind of chemical bond binds the hydrogen and oxygen in a water molecule?
(e) How could you calculate the energy released when H2 and O2 combine to form water?
(f) What is an antisymmetric wavefunction?
(g) What is the exchange energy?
Problem 2
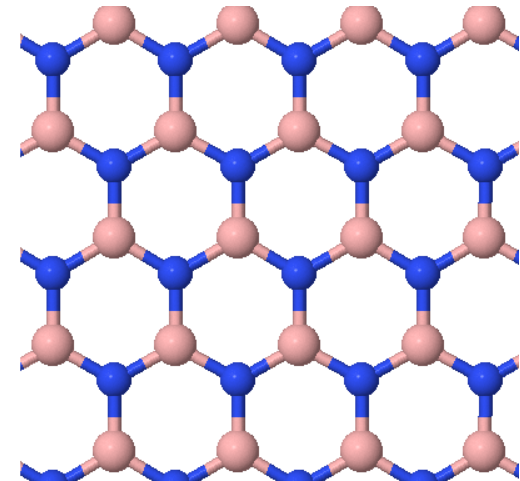
Hexagonal boron-nitride (hBN) is a two-dimensional material with a hexagonal Bravais lattice and two atoms in the basis.

(a) Draw primitive lattice vectors in the drawing above.
(b) Draw the Wigner-Seitz cell in the drawing above.
(c) Let $a$ be the distance between boron atoms in the lattice. What are the primitive lattice vectors in reciprocal space in terms of $a$.
(d) Draw the first Brillouin zone of this crystal.
(e) In Low Energy Electron Diffraction (LEED) electrons diffract off a surface. From a LEED pattern it is possible determine how the atoms are arranged on the surface. How would the reciprocal lattice vectors be determined from a LEED measurement?
(f) How many acoustic phonon modes and how many optical phonon modes does a single layer of hBN have?
(g) Sketch the phonon dispersion curves for hBN.
(h) How can the speed of sound in hBN be determined from the phonon dispersion curves?
Problem 3
Germanium is a semiconductor with a band gap of 0.66 eV. The crystal structure is diamond and the Bravais lattice is fcc. A light hole band and a heavy hole band have the same maximum at the $\Gamma$ point and the minimum of the conduction band lies betwen $\Gamma$ and $L$.
(a) Draw the electronic band structure ($E$ vs. $k$) of germanium.
(b) What is the chemical potential of Ge at low temperature?
(c) Describe how you could determine the electronic density of states of Ge. Make a sketch of the electronic density of states near the band edges.
(d) What is the temperature dependence of the specific heat of Ge at low temperature?
Quantity | Symbol | Value | Units | |
| electron charge | e | 1.60217733 × 10-19 | C | |
| speed of light | c | 2.99792458 × 108 | m/s | |
| Planck's constant | h | 6.6260755 × 10-34 | J s | |
| reduced Planck's constant | $\hbar$ | 1.05457266 × 10-34 | J s | |
| Boltzmann's constant | kB | 1.380658 × 10-23 | J/K | |
| electron mass | me | 9.1093897 × 10-31 | kg | |
| Stefan-Boltzmann constant | σ | 5.67051 × 10-8 | W m-2 K-4 | |
| Bohr radius | a0 | 0.529177249 × 10-10 | m | |
| atomic mass constant | mu | 1.6605402 × 10-27 | kg | |
| permeability of vacuum | μ0 | 4π × 10-7 | N A-2 | |
| permittivity of vacuum | ε0 | 8.854187817 × 10-12 | F m-1 | |
| Avogado's constant | NA | 6.0221367 × 1023 | mol-1 |