First name
Last name
Matrikelnr.
Problem 1
The many particle Hamiltonian for any molecule or solid is,
\begin{equation} \label{eq:htotal} H_{\text{mp}}= -\sum\limits_i \frac{\hbar^2}{2m_e}\nabla^2_i -\sum\limits_a \frac{\hbar^2}{2m_a}\nabla^2_a -\sum\limits_{a,i} \frac{Z_ae^2}{4\pi\epsilon_0 |\vec{r}_i-\vec{r}_a|}+\sum\limits_{i< j} \frac{e^2}{4\pi\epsilon_0 |\vec{r}_i-\vec{r}_j|}+\sum\limits_{a< b} \frac{Z_aZ_be^2}{4\pi\epsilon_0 |\vec{r}_a-\vec{r}_b|} . \end{equation}An approximate solution of the many-electron Hamiltonian for a molecule can be found by applying the Born-Oppenheimer approximation and neglecting the electron-electron interactions. The resulting Hamiltonian is called the reduced Hamiltonian. The reduced Hamiltonian is the sum of $N_e$ identical molecular orbital Hamiltonians where $N_e$ is the number of electrons in the molecule.
\begin{equation} H_{\text{red}}= \sum \limits_{i=1}^{N_e} H_{\text{mo}}. \end{equation}(a) Explain what the Born-Oppenheimer approximation is and why it is possible to use this approximation.
Acetylene C2H2 consists of two carbon atoms ($Z=6$) at positions $\vec{r}_{C1}$, $\vec{r}_{C2}$ and two hydrogen atoms ($Z=1$) at positions $\vec{r}_{H1}$, $\vec{r}_{H2}$.

(b) What is the molecular orbital Hamiltonian for acetylene?
$H_{\text{mo}}=$
(c) In the linear combination of atomic orbitals, what trial wave function would you use to solve the molecular orbital Hamiltonian for acetylene? Write the atomic orbitals in a format like $\phi_{1s}^\text{H}(\vec{r}-\vec{r}_{H1})$.
$\psi_{\text{mo}}=$
(d) How many of the molecular orbitals that will be calculated with your trial wave function from part (c) will be occupied in the ground state of acetylene?
(e) How many vibrational and how many rotational modes does an acetylene molecule have?
First name
Last name
Matrikelnr.
Problem 2
This image shows the CsCl crystal structure. The lattice parameters of the conventional unit cell are given in the figure.
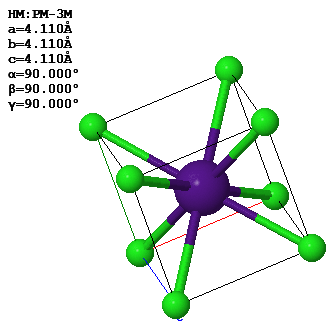
(a) What is the closest distance between a Cs atom and a Cl atom?
(b) Draw the (110) plane of CsCl. Put the drawing there →.
(c) What are the primitive lattice vectors in reciprocal space?
$\vec{b}_1=$
$\vec{b}_2=$
$\vec{b}_3=$
(d) What is the length of the reciprocal lattice vector $\vec{G}_{111}$?
The atomic form factors for Cs and Cl are:
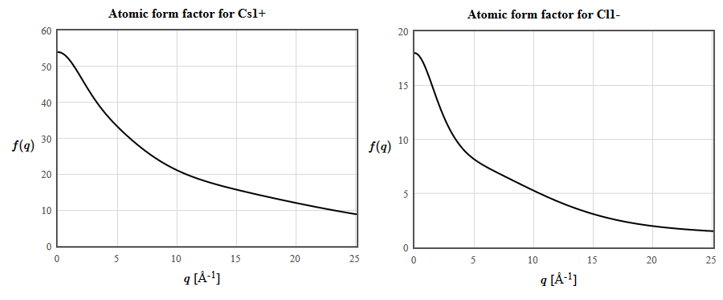
(e) The horizontal axis is the scattering vector $\vec{q}= \vec{k}'-\vec{k}$. What is the structure factor of $\vec{G}_{111}$?
Problem 3
The phonon dispersion relation of GaN is shown below.
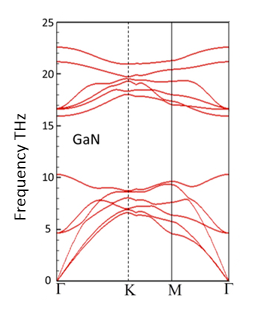
(a) How many atoms are there in the basis of GaN?
(b) How does symmetry help find the form of the normal modes? Write down the formula for the normal modes.
(c) What is the frequency and the wavelength of the optical mode with the lowest frequency at the Γ point.
Below is the phonon density of states of GaN.
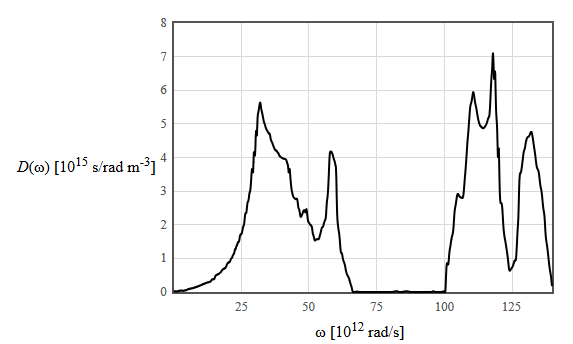
(d) What is the density of occupied phonon states in a frequency interval $\Delta \omega=10^4$ [rad/s] centered at an angular frequency of $50 \times 10^{12}$ rad/s at 300 K?
Problem 4
(a) Using the empty lattice approximation, draw the electronic band structure of a bcc metal.

(b) This metal has one valence electron per unit cell. Include the Fermi energy in your drawing.
(c) $E=0$ is indicated in the plot. What is approximately the Fermi energy in electron volts if the lattice constant is $a=4.3$ Å? (You can estimate $E_F$ if you calculate the energies where the dispersion curve meets the Brillouin zone boundaries.)
The density of states for a particular material is given in the following figure. The total electron density is $14 \times 10^{28}$ electrons/m³. The form of the density of states was chosen to make it easy to integrate (by counting squares).

(d) Is this material a metal, an insulator, or a semiconductor? Why?
(e) What is the limiting value of the Fermi energy as the temperature approaches zero?
Quantity | Symbol | Value | Units | |
| electron charge | e | 1.60217733 × 10-19 | C | |
| speed of light | c | 2.99792458 × 108 | m/s | |
| Planck's constant | h | 6.6260755 × 10-34 | J s | |
| reduced Planck's constant | $\hbar$ | 1.05457266 × 10-34 | J s | |
| Boltzmann's constant | kB | 1.380658 × 10-23 | J/K | |
| electron mass | me | 9.1093897 × 10-31 | kg | |
| Stefan-Boltzmann constant | σ | 5.67051 × 10-8 | W m-2 K-4 | |
| Bohr radius | a0 | 0.529177249 × 10-10 | m | |
| atomic mass constant | mu | 1.6605402 × 10-27 | kg | |
| permeability of vacuum | μ0 | 4π × 10-7 | N A-2 | |
| permittivity of vacuum | ε0 | 8.854187817 × 10-12 | F m-1 | |
| Avogado's constant | NA | 6.0221367 × 1023 | mol-1 |