First name
Last name
Matrikelnr.
Problem 1
Carbon monoxide is a diatomic molecule consisting of one carbon atom $(Z=6)$ and one oxygen atom $(Z=8)$.
(a) The energies of the first few molecular orbitals (starting with the molecular orbital with the lowest energy) of CO are $E_1=-564.05$ eV, $E_2=-309.81$ eV, $E_3=-42.65$ eV, $E_4=-21.96$ eV, $E_5= -18.15$ eV, $E_6=-18.15$ eV, $E_7= -15.56$ eV, $E_8= 3.47$ eV, $E_9= 3.47$ eV, $E_{10}=6.38$ eV. Which of these molecular orbitals are occupied?
(b) A carbon monoxide molecule absorbs a photon that promotes an electron from the highest occupied molecular orbital to the lowest unoccupied molecular orbital. What is the energy of this photon?
(c) Write down a trial wavefunction that could be used to determine the molecular orbitals by the Linear Combination of Atomic Orbitals method.
$\psi_{\text{mo}}=$
(d) How many vibrational modes does CO have?
(e) Explain how you could calculate the smallest energy photon that CO could absorb by making a transition between rotational states if you knew values for the masses $m_{\text{C}}$, $m_{\text{O}}$ and the bond length $r_0$.
Problem 2
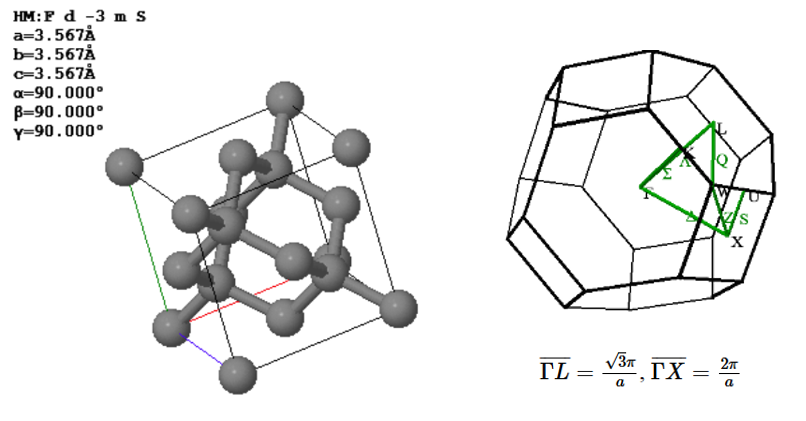
Diamond has an fcc Bravais lattice. The primitive lattice vectors are,
$\vec{a}_1=\frac{a}{2}\hat{x}+\frac{a}{2}\hat{y}$, $\vec{a}_2=\frac{a}{2}\hat{x}+\frac{a}{2}\hat{z}$, $\vec{a}_3=\frac{a}{2}\hat{y}+\frac{a}{2}\hat{z}$.
There are two atoms in the basis. The positions of the two carbon atoms given in terms of the fractional coordinates of the conventional unit are,
$\vec{B}_1=(0,0,0)$, $\vec{B}_2=(0.25,0.25,0.25)$.

(a) Draw the arrangement of the carbon atoms in the (110) plane using the Miller indices of the conventional unit cell. Label the directions in your drawing with Miller indices. Indicate the distance bewteen the atoms in the two perpendicular directions.
(b) The closest point on the Brilluoin zone boundary to $\Gamma$ is $L$. What is the maximum wavelength photon that can be diffracted from a diamond crystal? $\overline{\Gamma L} = \frac{\sqrt{3}\pi}{a}$
(c) How many $k$ vectors satisfy periodic boundary conditions for a diamond crystal 1 cm³ (The lattice constant is $a=3.567$ Å.)
First name
Last name
Matrikelnr.
(d) The lattice vibrations can be described in terms of normal modes. How many normal modes does a diamond crystal 1 cm³ have?
(e) Sketch approximately the phonon dispersion relation for diamond along $L-\Gamma -X$.
(f) Diamond is an electrical insulator with a band gap of 5.5 eV. Which frequencies of light would diamond absorb?
(g) Draw approximately the electronic density of states near the top of the valence band and bottom of the conduction band. The effective mass of the electrons is greater than the effective mass of the holes. Include the chemical potential in your drawing.
Problem 3
The density of states for a particular material is given in the following figure. The total electron density is $12 \times 10^{28}$ electrons/m³. The form of the density of states was chosen to make it easy to integrate (by counting squares).
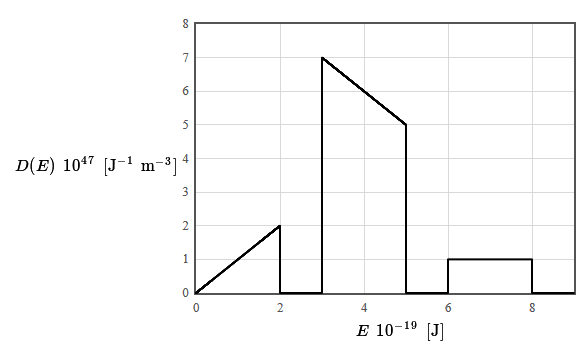
(a) Is this material a metal, an insulator, or a semiconductor? Why?
(b) What is the limiting value of the Fermi energy as the temperature approaches zero?
(c) The specific heat of a metal can be fit to the form $c_v=\gamma T + AT^3$ at low temperatures. Here $\gamma$ and $A$ are constants and $T$ is the absolute temperature. What is the temperature dependence of the electronic component of the internal energy density and the phonon component of the internal energy density at low temperature?
(d) Plot the derivative of the Fermi function as a function of energy and explain why the shape of this function is relevant for the calculation of properties such the specific heat or the electrical conductivity of metals.
(e) What is the Wiedemann–Franz law?
(f) The chemical potential of a metal is weakly temperature dependent so it can be estimated by calculating the Fermi energy. A monovalent metal has a simple cubic lattice and a lattice constant of $a= 0.1$ nm. Use the free electron model to estimate the chemical potential in this case.
Quantity | Symbol | Value | Units | |
| electron charge | e | 1.60217733 × 10-19 | C | |
| speed of light | c | 2.99792458 × 108 | m/s | |
| Planck's constant | h | 6.6260755 × 10-34 | J s | |
| reduced Planck's constant | $\hbar$ | 1.05457266 × 10-34 | J s | |
| Boltzmann's constant | kB | 1.380658 × 10-23 | J/K | |
| electron mass | me | 9.1093897 × 10-31 | kg | |
| Stefan-Boltzmann constant | σ | 5.67051 × 10-8 | W m-2 K-4 | |
| Bohr radius | a0 | 0.529177249 × 10-10 | m | |
| atomic mass constant | mu | 1.6605402 × 10-27 | kg | |
| permeability of vacuum | μ0 | 4π × 10-7 | N A-2 | |
| permittivity of vacuum | ε0 | 8.854187817 × 10-12 | F m-1 | |
| Avogado's constant | NA | 6.0221367 × 1023 | mol-1 |