Exercise Exam 25.06.2019

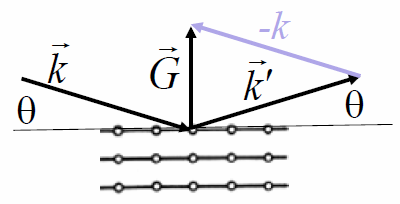
1. A neutron beam with an energy of 0.06 eV diffracts from a crystal. The incoming neutron beam has a wave vector $\vec{k}$ and the diffracted beam has a wave vector $\vec{k}'$. A diffraction peak will be observed every time the diffraction condition is satisfied, $\vec{k}' - \vec{k} = \vec{G}$. One of the diffraction peaks that is observed corresponds to a reciprocal lattice vector $|\vec{G}| = 2.23$ Å^-1. What is the distance between the net planes for this reciprocal lattice point? The net planes are always normal to the reciprocal lattice vector. What is the diffraction angle $\theta$ that $\vec{k}$ makes with the net planes?

Solution

2. Sodium is a metal so there is an electron contribution and a phonon contribution to the specific heat. At high temperatures, the electron contribution increases with temperature but the phonon contribution is constant. The atomic density of sodium is $n=\frac{N}{V}=2.54 \times 10^{28}\text{ m}^{-3}$ and the Debye temperature is $\theta_D=156 \text{ K}$. Sodium is monovalent.

(a) Calculate the total specific heat (due to both the electrons and the phonons) at 10 K.

(b) Use Dulong Petit law to approximate the specific heat at 300 K. Is the electron contribution negligible at this temperature?

Solution

<hr />

(a) In the <a href="http://lampz.tugraz.at/~hadley/ss1/fermigas/electrontable/electrontable.html">Free electron model</a>, the specific heat is,

$$c_{v,el}=\frac{\pi^2D(E_F)}{3}k_B^2T = \frac{\pi^2n}{2E_F}k_B^2T$$

Here $E_F$ is the Fermi energy and $D(E_F)$ is the density of states at the Fermi energy,

$E_F =5.05 \times 10^{-19}\text{ J} = 3.15$ eV.

At 10 K, the electronic contribution to the specific heat is,
$c_{v,el} = $ 473 J K-1 m-3.

The low temperature form of the phonon contribution to the specific heat in the Debye approximation is,

\[ \begin{equation} 
c_v\approx \frac{12\pi^4}{5}k_Bn\left(\frac{T}{\Theta_D}\right)^3\quad\left[\text{J K}^{-1}\text{m}^{-3}\right]\qquad \text{For}\quad T << \Theta_D
\end{equation} \]

$c_{v,ph} = $ 21600 J K-1 m-3.

The total specific heat at 10 K is,

$c_{v} = $ 22100 J K-1 m-3.

(b) To estimate the phonon contribution to the specific heat at high temperatures, the Dulong-Petit law can be used,

$c_{v,ph} \approx 3nk_B =$ 1.05 × 106 J K-1 m-3.

At 300 K, the electron contribution is $c_{v,e1} =$ 14200 J K-1 m-3 which is much smaller than the phonon contribution at 300 K.

Some thermodynamic properties of the elements can be found at <a href="http://lampz.tugraz.at/~hadley/ss1/materials/sgte/SGTE.html">http://lampz.tugraz.at/~hadley/ss1/materials/sgte/SGTE.html</a>. The specific heat of sodium has the form,

The spike in $c_p$ is due to solid-liquid phase transition.

3. An electron density of states plot is shown below shown below. The form of the density of states was chosen to make it easy to integrate (by counting squares).

For each of these two electron densities,

(a) $13\times 10^{28}$ electrons/m³
(b) $17\times 10^{28}$ electrons/m³

state whether this material is a metal, an insulator, or a semiconductor and give the Fermi energy.

Solution