Exercise Exam 14.05.2019

1. The bond potential of a diatomic molecule has the form, $U(R)=-\frac{A}{ R^2}+\frac{B}{ R^{10}}$. The bondlength of this molecule is 2.8 Å and the dissociations energy is 8 eV.

Calculate $A$ and $B$.

Solution

(2a) If the ground state potential of the HCl molecule in the vicinity of the minimum is approximated by $E_{pot} = \frac{k (R- R_e)^2}{2}$, one obtains a vibration frequency of $\nu_0 = 9 \times 10^{13}\, \text{s}^{-1}$. Calculate the constant $k$. What is the classical oscillation amplitude for an oscillation with the same energy as the $\nu = 1$ state? $m_H = 1 u$, $m_Cl = 35.45 u$, $u = 1.66 \times 10^{-27}$ kg.

(2b) For the normal modes of a molecule, the following energies were found: 0.18678 eV and $1.05344 \times 10^{-19}$ J. Calculate the corresponding frequencies and wavelengths.

Solution

<hr />

(a) The vibrational frequency is $\nu_0=9\times 10^{13}\,\text{Hz} = \frac{1}{2\pi}\sqrt{k/m_r}$, where $k$ is the spring constant and $m_r=(1/m_a+1/m_b)^{-1}$ is the reduced mass.

mr_HCl = 1/(1/(m_H*u) + 1/(m_Cl*u));
k_HCl = (mr_HCl*(4*Math.PI*Math.PI*f_HCl*f_HCl)).toPrecision(3);
//document.write("The spring constant for a HCl molecule is "+k_HCl+" N/m.<\/p>");

</script>

The spring constant for a HCl molecule is 521 N/m.

The energy for $\nu=1$ is $hf(\nu+1/2) = 8.945\times 10^{-20}\,\text{J}$. Classically, this energy is $\frac{kA^2}{2}$ where $A$ is the amplitude. 
$A = \sqrt{\frac{2\times 8.945\times 10^{-20}}{521}}=1.853\times 10^{-11}$ m.

(b) For 0.18678 eV the frequency is $4.516\times 10^{13}$ Hz and the wavelength is 6.638 μm.
For 1.05344E-19 J the frequency is $1.590\times 10^{14}$ Hz and the wavelength is 1.886 μm.

(3) As part of a space program, the Saturn atmosphere is to be examined for CO. The examination has to be executed from the orbit of a satellite with a microwave apparatus. $m_{C12} = 12 u$, $m_{C13} = 13 u$, $m_O = 16 u$, $u = 1.66 \times 10^{-27}$ kg.

(a) At which frequencies are the first four rotational transitions for ¹²C¹⁶O for a given bond length of 112.82 pm?

(b) In order to determine the relative abundance of the ¹³C-isotope, the 1 → 0 transition of the corresponding molecules must still be resolved. Calculate the energy difference of this transition for the two C-isotopes.

Solution

<hr />

(a) The energies of the rotational states are,

$$E_J = \frac{\hbar^2}{2I}J(J+1)\qquad J= 0,1,2,\cdots$$

where $I$ is the moment of inertia,

$$I=\frac{m_Cm_O}{m_C+m_O}r_0^2.$$
Since $J= \pm 1$ in a transition, the frequencies of the first four would be:

$$f = \frac{\hbar}{2\pi I}(J+1)\qquad J= 0,1,2,3$$

m_C12 = 12*u;
m_C13 = 13*u;
m_O = 16*u;
mu= m_C12*m_O/(m_C12+m_O);
mu13 = m_C13*m_O/(m_C13+m_O);
r0 = 112.82E-12;
I12 = mu*r0*r0;
I13 = mu13*r0*r0;

//for (J=0; J<4; J++) {
// f = (hbar/(2*Math.PI*I12))*(J+1);
// document.write("For J="+(J+1)+" → J="+J+", the frequency is "+f.toPrecision(3)+" Hz.<br\/>");
//}
</script>

For J=1 → J=0, the frequency is $1.16\times 10^{11}$ Hz.

For J=2 → J=1, the frequency is $2.32\times 10^{11}$ Hz.

For J=3 → J=2, the frequency is $3.47\times 10^{11}$ Hz.

For J=4 → J=3, the frequency is $4.63\times 10^{11}$ Hz.

(b) For 12C16O, the frequency of the 1 → 0 transition is $1.1581\times 10^{11}$ Hz.

For 13C16O, the frequency of the 1 → 0 transition is $1.1072\times 10^{11}$ Hz.

The energy difference is $3.37\times 10^{-24}$ J = 0.021 meV.

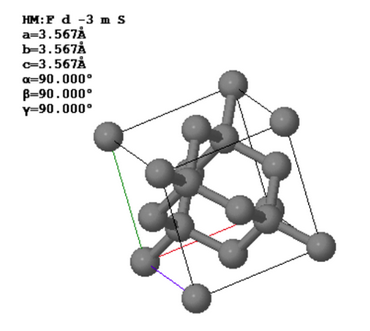
Diamond has an fcc Bravais lattice. The primitive lattice vectors are,

$\vec{a}_1=\frac{a}{2}\hat{x}+\frac{a}{2}\hat{y}$, $\vec{a}_2=\frac{a}{2}\hat{x}+\frac{a}{2}\hat{z}$, $\vec{a}_3=\frac{a}{2}\hat{y}+\frac{a}{2}\hat{z}$.

There are two atoms in the basis. The positions of the two carbon atoms given in terms of the fractional coordinates of the conventional unit are,

$\vec{B}_1=(0,0,0)$, $\vec{B}_2=(0.25,0.25,0.25)$.

(a) Draw the arrangement of the carbon atoms in the (110) plane using the Miller indices of the conventional unit cell. Label the directions in your drawing with Miller indices. Indicate the distance between the atoms in the two perpendicular directions.

(b) Calculate the volume of the primitive unit cell.

Solution