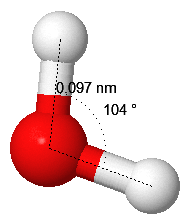
513.001 Molecular and Solid State Physics
11.04.2016

Problem 1

The many particle Hamiltonian for any molecule is,

\begin{equation} \label{eq:htotal} H_{\text{mp}}= -\sum\limits_i \frac{\hbar^2}{2m_e}\nabla^2_i -\sum\limits_a \frac{\hbar^2}{2m_a}\nabla^2_a -\sum\limits_{a,i} \frac{Z_ae^2}{4\pi\epsilon_0 |\vec{r}_i-\vec{r}_a|}+\sum\limits_{i< j} \frac{e^2}{4\pi\epsilon_0 |\vec{r}_i-\vec{r}_j|}+\sum\limits_{a< b} \frac{Z_aZ_be^2}{4\pi\epsilon_0 |\vec{r}_a-\vec{r}_b|} . \end{equation}

(a) What is the Born-Oppenheimer approximation? Why is this approximation valid?

Water H2O consists of two hydrogen atoms ($Z=1$) and one oxygen atom ($Z=8$). The molecular orbital Hamiltonian for water describes the motion of a single electron. What is the molecular orbital Hamiltonian for water?

(b) Use a linear combination of atomic orbitals to write down an approximate wave function that solves the molecular orbital Hamiltonian for water.

(c) How could you calculate the rotational energy states of water?

Problem 2
The primitive lattice vectors of a two dimensional sheet of hexagonal boron nitride are,

\[ \begin{equation} \vec{a}_1=\frac{\sqrt{3}}{2}a\hat{x}+\frac{a}{2}\hat{y},\quad\vec{a}_2=\frac{\sqrt{3}}{2}a\hat{x}-\frac{a}{2}\hat{y}. \end{equation} \].

Here $a=2.5$ Å.

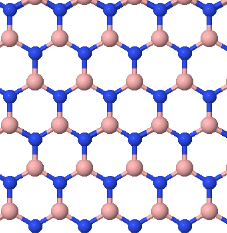
(a) Draw the Wigner-Seitz primitive unit cell.

(b) How many atoms are there in a primitive unit cell?

(c) What are the reciprocal lattice vectors of hexagonal boron nitride?

Problem 3
The speed of sound in copper is 3560 m/s. The crystal structure is fcc and the lattice constant (of the conventional unit cell) is 361.5 pm. The point farthest from $\Gamma$ on the first Brillouin zone boundary is the symmetry point W where $\overline{\Gamma W}=\sqrt{5}\pi/a$.

\[ \begin{equation} \large \overline{\Gamma L}=\frac{\sqrt{3}\pi}{a},\quad\overline{\Gamma X}=\frac{2\pi}{a},\quad\overline{\Gamma W}=\frac{\sqrt{5}\pi}{a}. \end{equation} \]

(a) Sketch the phonon dispersion relation for copper along $L- \Gamma - W$.

(b) Explain what the Debye frequency is and estimate it for copper.

Problem 4
Chrome has a bcc lattice and a lattice constant of $a=$ 0.291 nm. There is one atom in the basis. Some distances between symmetry points in the first Brillouin zone are,

\[ \begin{equation} \large \overline{\Gamma N}=\frac{\sqrt{2}\pi}{a},\quad\overline{\Gamma P}=\frac{\sqrt{3}\pi}{a},\quad\overline{\Gamma H}=\frac{2\pi}{a}. \end{equation} \]

(a) Sketch the electron dispersion relation for chrome along $N- \Gamma - P$.

(b) The chemical potential of a metal is weakly temperature dependent so it can be estimated by calculating the Fermi energy. How could the free electron model be used to estimate the chemical potential in this case?

(c) How could the free electron model be used to estimate the electronic contribution to specific heat of chrome?